
复数
数集拓展到范围内,仍有些运算无法进行。比如判别式小于0的一元二次方程仍无解,因此将数集再次扩充,达到复数范围。
形如z=a+bi的数称为复数(complex number),其中规定i为虚数单位,且i^2=i×i=-1(a,b是任意实数)。我们将复数z=a+bi中的实数a称为复数z的实部(real part)记作Rez=a,实数b称为复数z的(imaginary part)记作 Imz=b。
已知:当b=0时,z=a,这时复数成为实数 当a=0且b≠0时,z=bi,我们就将其称为
共轭复数
对于复数z=a+bi,称复数z'=a-bi为z的共轭复数。即两个实部相等,虚部(虚部不等于0)互为的复数互为共轭复数(conjugate complex number)。复数z的共轭复数记作z。表示方法为在字母z上方加一横线即共轭符号。
复数的运算
加法
z1=a1+b1i, z2=a2+b2i
z1+z2 = (a1+b1i)+(a2+b2i) = (a1+a2)+(b1+b2)i
乘法
z1=a1+b1i, z2=a2+b2i
z1*z2=(a1+b1i)*(a2+b2i)
= (a1a2-b1b2)+(a1b2+a2b1)i
除法
z1=a1+b1i, z2=a2+b2i
z1/z2 = [(a1a2 + b1b1) + (a2b1-a1b2)i]/(a2a2 + b2b2)
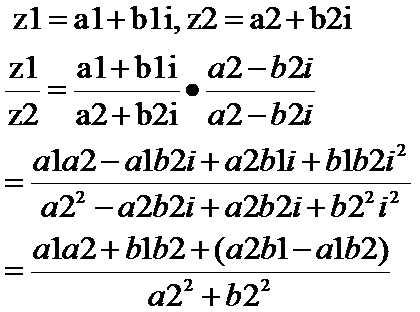
复数的模
将复数的实部与虚部的和的正的的值称为该复数的模,记作∣z∣. 即对于复数z=a+bi,它的模 ∣z∣=√(a^2+b^2)
棣莫佛定理
对于复数z=r(cosθ+isinθ),有z的n次幂
z^n=(r^n)*[cos(nθ)+isin(nθ)] (其中n是)
开方法则
若z^n=r(cosθ+isinθ),则
z=n√r[cos(2kπ+θ)/n+isin(2kπ+θ)/n](k=0,1,2,3……n-1)
模拟复数及其运算的源码实现
package cn.edu.jxau.image;/** * 用y = a+bi;模拟复数 * @author luoweifu * */class Complex { private double a; private double b; public Complex(double a, double b) { this.a = a; this.b = b; } public double getA() { return a; } public double getB() { return b; } /** * 求一个复数和一个实型数据的和; * @param a 实数 * @return 结果(复数) */ public Complex add(double a) { this.a = this.a + a; return this; } /** * 用于求解两复数的和 * z1=a1+b1i, z2=a2+b2i * z1+z2 = (a1+a2) + (b1+b2)i * @param c * @return */ public Complex add(Complex c) { a = a + c.getA(); b = b + c.getB(); return this; } /** * 用于求一个复数和一个实型数据的差; * @param x * @return */ public Complex minus(double x) { a = a-x; return this; } /** * 用于求解两复数的差 * @param c * @return */ public Complex minus(Complex c) { a = a - c.getA(); b = b - c.getB(); return this; } /** * 用于求一个复数和一个实型数据的积; * @param r * @return */ public Complex multiply(double r) { a = a* r; b = b*r; return this; } /** * 复数的乘法 * z1=a1+b1i, z2=a2+b2i * z1*z2 = (a1+b1i)*(a2+b2i)= (a1a2-b1b2) + (a1b2+a2b1)i * @param c * @return */ public Complex multiply(Complex c) { double a1 = this.a, b1 = this.b; double a2 = c.getA(), b2 = c.getB(); a = a1*a2 - b1*b2; b = a1*b2+a2*b1; return this; } /** * 复数的除法 * z1=a1+b1i, z2=a2+b2i * z1/z2 = [(a1a2 + b1b1) + (a2b1-a1b2)i]/(a2a2 + b2b2) * @param c * @return */ public Complex division(Complex c) { double a1 = this.a, b1 = this.b; double a2 = c.getA(), b2 = c.getB(); a = (a1*a2 + b1*b2)/(a2*a2 + b2*b2); b = (a2*b1 - a1*b2)/(a2*a2 + b2*b2); return this; } @Override public String toString() { if(b>=0) { return a + "+" + b + "i"; } else { return a + "" + b + "i"; } } /** * 求复数的模 * @return */ public double model() { return Math.sqrt(a*a + b*b); } /** * 复数的n次幂 * @param n * @return */ public Complex pow(int n) { double r = model(); double o = Math.atan2(b, a); a = Math.pow(r, n)*Math.cos(n*o); b = Math.pow(r, n)*Math.sin(n*o); return this; } /* public double sqrt(int n) { double r = model(); double o = Math.atan2(b, a); //Math. return 0; } */ /*public static void main(String[] args) { Complex c1 = new Complex(5, 3); Complex c2 = new Complex(1, 2); c1.add(4); System.out.println("复数(5+3i)与实数4的和为:"+c1); c1.add(c2); System.out.println("复数(5+3i)与复数(1+2i)的和为:"+c1); c1.minus(4); System.out.println("复数(5+3i)与实数4的差为:"+c1); c1.minus(c2); System.out.println("复数(5+3i)与复数(1+2i)的差为:"+c1); c1.multiply(7); System.out.println("复数(5+3i)与实数7的积为:"+c1); c1.multiply(c2); System.out.println("复数(5+3i)与复数(1+2i)的积为:"+c1); c1.division(c2); System.out.println("复数(5+3i)与复数(1+2i)的商为:"+c1); //System.out.println(Math.pow(81, 0.25)); }*/ } 复数的几何表示法
①形式
复数z=a+bi 被复平面上的点 z(a,b )唯一确定。这种形式使复数的问题可以借助图形来研究。也可反过来用复数的理论解决一些几何问题。
②形式。复数z=a+bi用一个以原点O为起点,点Z(a,b)为终点的向量OZ表示。这种形式使复数四则运算得到恰当的几何解释。
③三角形式。复数z=a+bi化为三角形式
z=r(cosθ+isinθ) 式中r= √(a^2+b^2),是复数的模(即)
θ 是以x轴为始边,OZ为终边的角,叫做复数的辐角,辐角的主值记作arg(z) 这种形式便于作复数的乘、除、乘方、运算。
④形式。将复数的三角形式z=r( cosθ+isinθ)中的cosθ+isinθ换为 exp(iθ),复数就表为指数形式z=rexp(iθ)